Introduction
Upper elementary students learn the standard algorithm for addition at some point during their elementary math instruction. It is generally the most efficient computational method, and it is essential for efficient multiplication computations later on in the curriculum. Teachers often introduce the algorithm conceptually by demonstrating the process with base ten blocks. Next, students solve addition computations pictorially using base ten block notation. Once students have success adding with pictures, teachers naturally transition to having students add with numbers.
The leap from the concrete pictorial demonstration, to the abstract numeric demonstration of the algorithm is greater than most teachers think. It is for this reason that students often have difficulty learning and retaining the process of the standard algorithm with numbers. I know from my experience as a Special Ed. Teacher and Math Interventionist, the number of upper elementary students who need remediation/intervention for addition computations is exorbitant.
The Missing Step – The Bridge Connecting Concrete and Abstract
To bridge the gap between the concrete and the abstract, the ‘Hybrid Method’ based on the picture book, The Good Neighbors Store an Award was created. This novel intervention incorporates digit/place value cards, and thumbnail illustrations to make the conceptual elements of the algorithm visible for students. The ‘Hybrid Method’ is Step 4 of the “5 ‘Novel’ Steps to Teach Addition with Regrouping – Conceptually”.



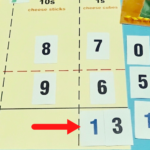
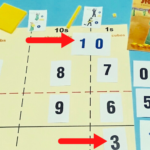
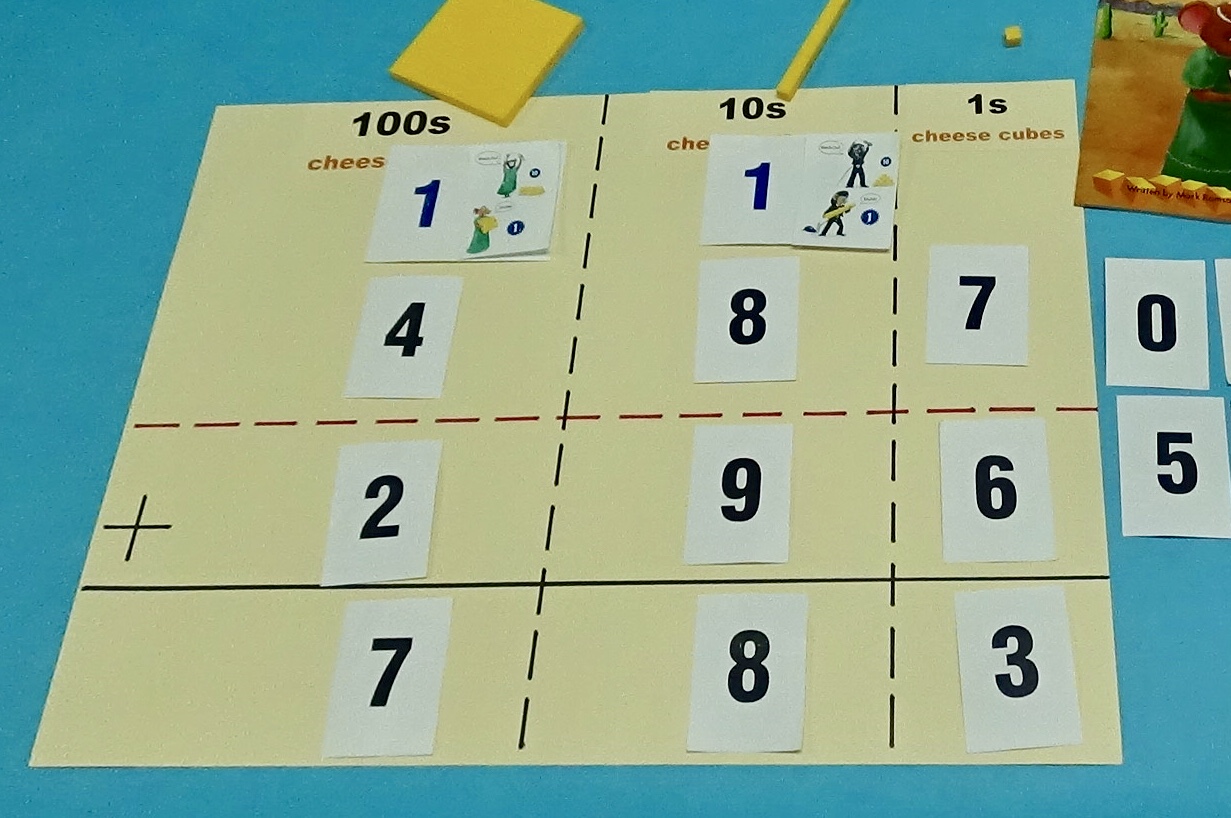
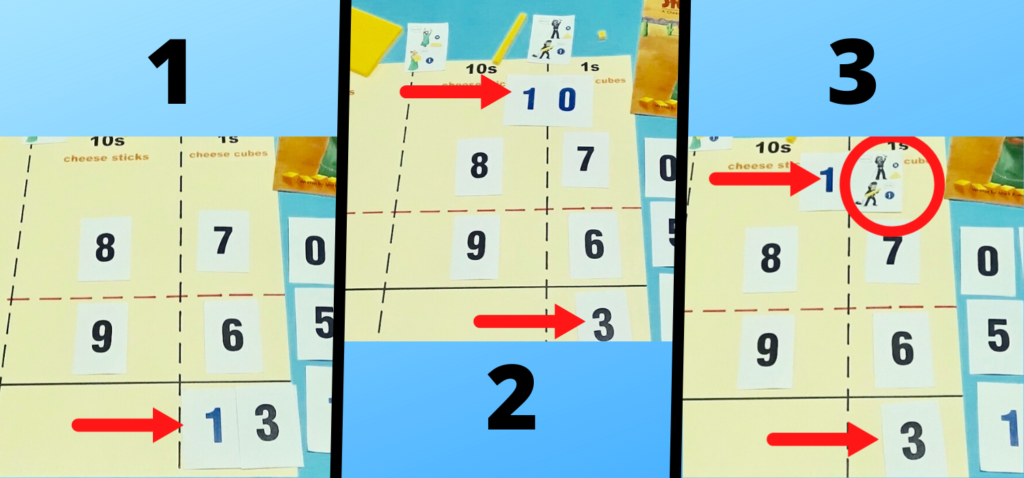
The cards are the key to the ‘Hybrid Method’. The 0-9 black digit cards and the blue 10 cards allow students to make the numbers 1-19 conceptually (ie.13 is made with the 10 card and the 3 card, 10+3=13, not a 1 card and a 3 card, 1+3=4). The two thumbnail illustration cards show the two different regrouping processes from the story. Each card shows the character melting 10 of his/her neighbor’s smaller sized blocks of cheese into 1 of his/her larger sized block of cheese (base ten block visual models).
When the cards are used in conjunction with each other, the addition with regrouping process comes alive. The regrouping process with the “Hybrid Method’ involves expanding numbers greater than 9 into tens and ones. The ones units remains in the original place value and the 10 units are moved to the next larger place value where they are turned into 1 of the larger unit. This is accomplished by placing the thumbnail card over the zero on the 10 card. The action of covering the zero on the 10 card with the thumbnail card makes the illustration on the thumbnail come to fruition – 10 smaller units were changed to 1 bigger unit. It is worthwhile to have students linger on this step. The newly acquired 1 unit is an additional addend to the original two. Then students can perform the addition for that given place value and the addition process continues on to the next place value(s) until the algorithm is complete. Students are encouraged to vocalize their actions as they perform the ‘Hybrid Method’ to further ingrain the process in their minds.
The action of covering the zero on the 10 card with the thumbnail card makes the illustration on the thumbnail come to fruition – 10 smaller units were changed to 1 bigger unit. It is worthwhile to have students linger on this step.
Conclusion
The ‘Hybrid Method’ combines visual, kinesthetic, numeric, and auditory/verbal modalities to provide an extraordinary learning expense for students. Because the ‘Hybrid Method’ is so effective, student generally need only a few times to perform it before they have a lasting conceptual understanding and can apply it to paper/pencil computations. The ‘Hybrid Method’ until now has been the missing step teachers needed to connect concrete and abstract understanding of addition with regrouping and the standard algorithm.