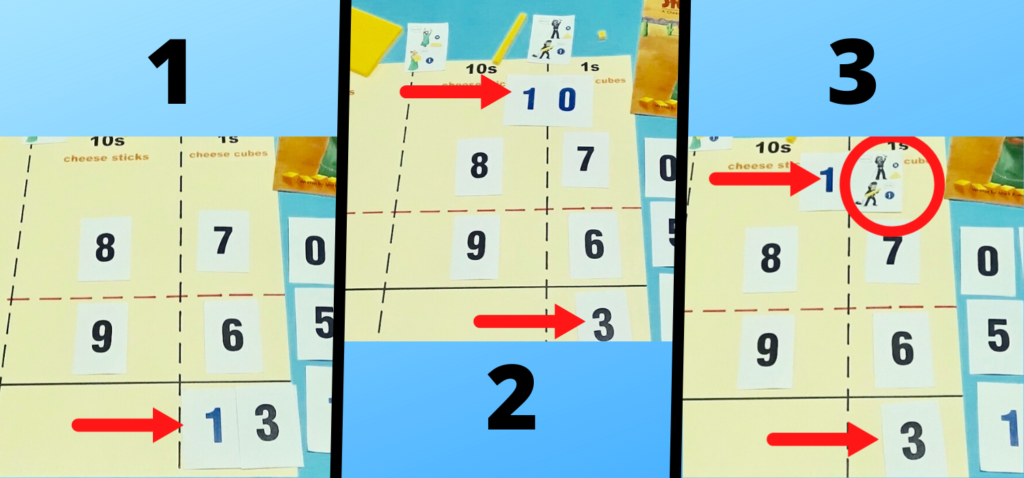
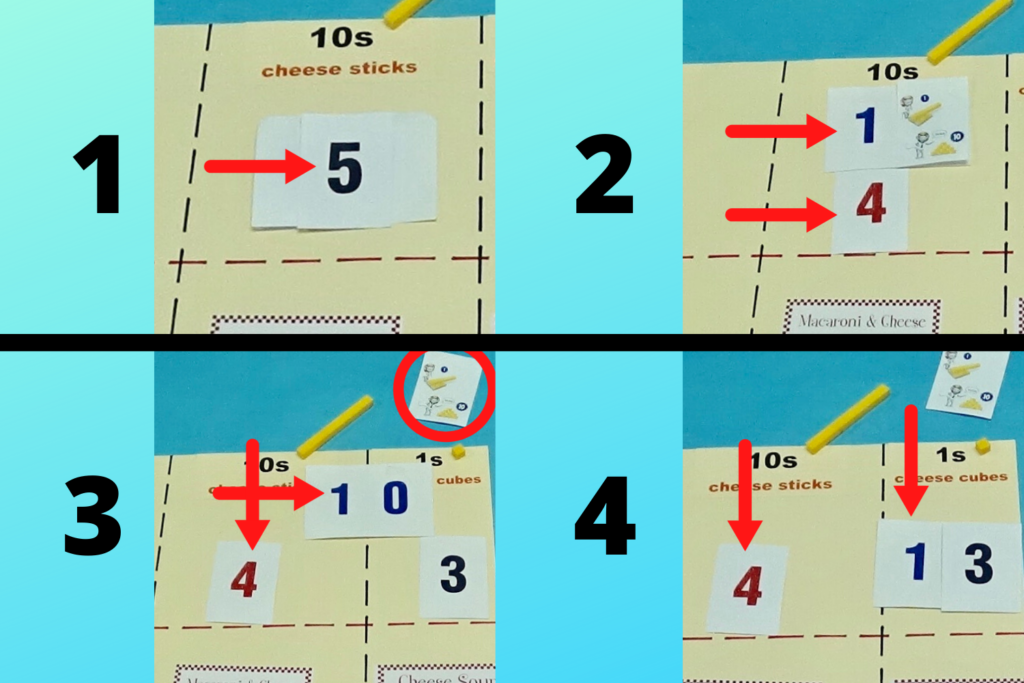
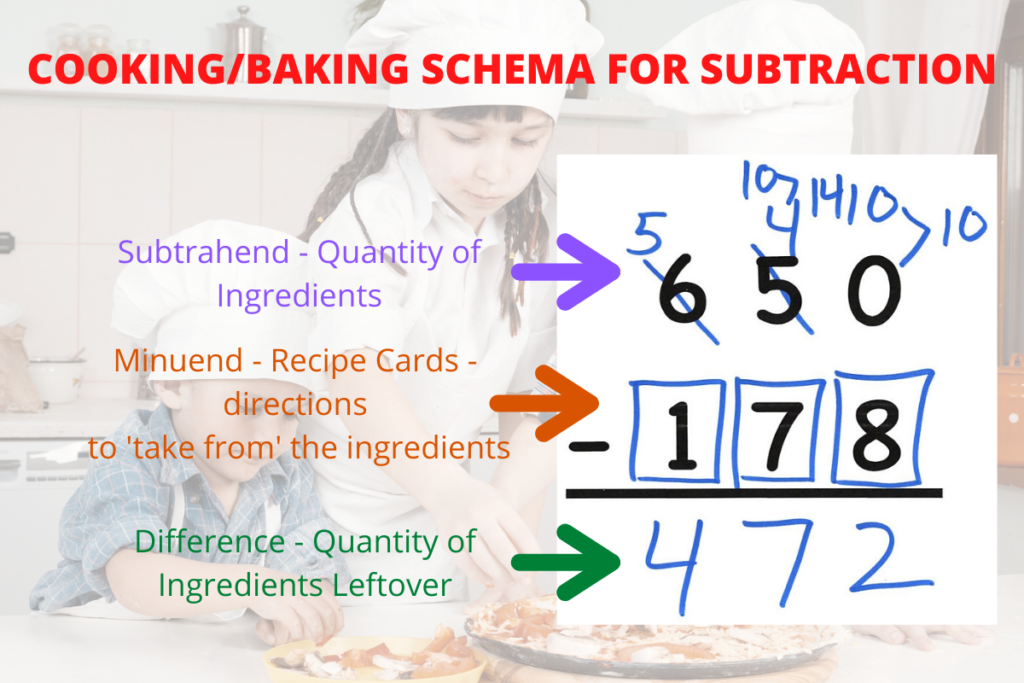
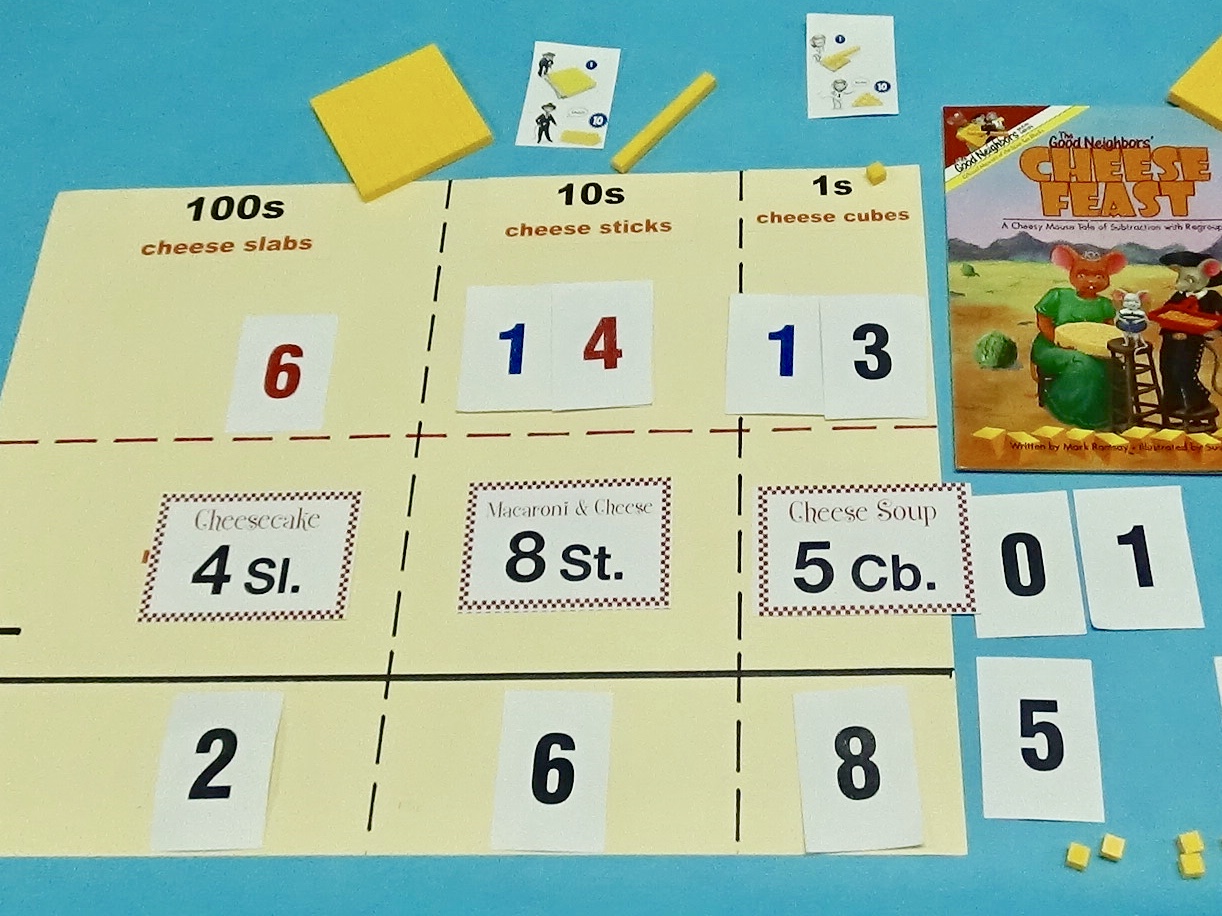
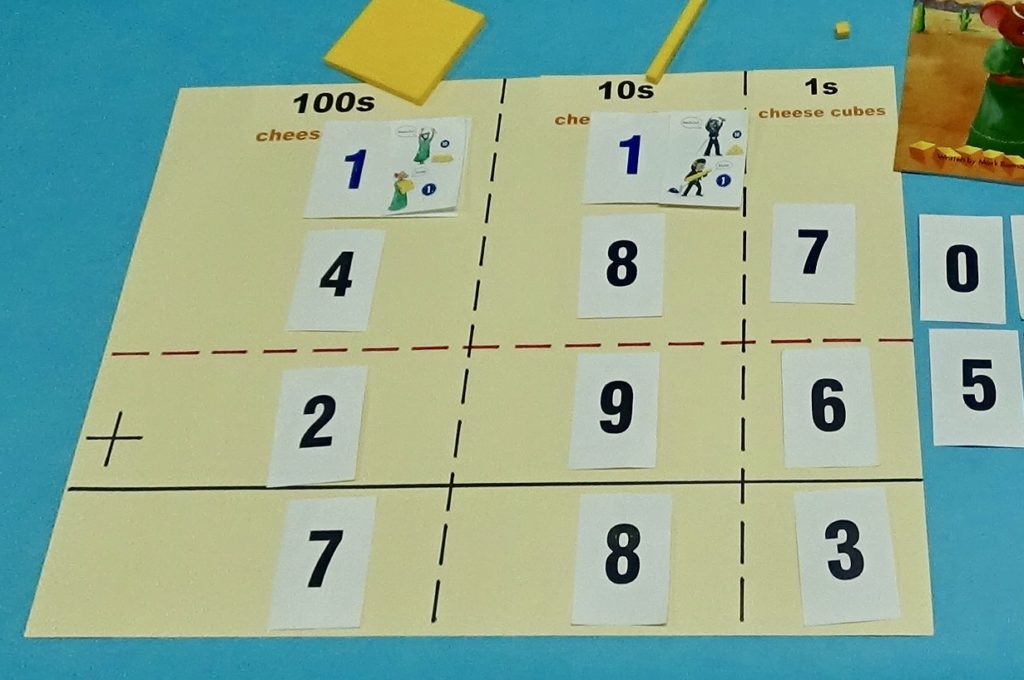
Instructional Scaffolding – Subtraction with Regrouping
Whether teachers realize it or not, they are continuously scaffolding instruction for their students. The dictionary definition of scaffolding is: a temporary structure on the outside of a building, made usually of wooden planks and metal poles, used by workers while building, repairing, or cleaning the building. This definition applies quite well to its’ educational connotation. Instructional scaffolding is temporary. It allows students to build, repair, and/or polish their understanding of concepts and skills. It is used temporarily to support students as they develop the required knowledge/skill needed to do something independently or progress to the next level of a skill.