Teaching the standard algorithm for subtraction may not be the first method of subtraction you teach students, but eventually every student should learn how to subtract using the standard algorithm. Conceptual understanding of the standard algorithms is the type of thinking that is needed to succeed in algebra and advanced mathematics (Wu 2009). The algorithm is based on place value understanding, and it is generally the most efficient subtraction strategy to use.
Look on Pinterest and you will see many beautiful pins of anchor charts with cute sayings and colorful pictures, but most of these strategies are just “tricks” or “gimmicks” that give students no true understanding of the process. With these “tricks” students are unable to explain how they are using place value and manipulating the numbers to subtract them together. Because the students have no true understanding of the process, errors often occur.
In this article, I will give you the 5 ‘Novel’ Steps I, a Special Education Teacher and Math Interventionist of over 25 years, use to teach students of all abilities the standard algorithm for subtraction. I call the steps ‘novel’ because all or some portion of each step is new to the teaching community as a whole.




STEP 1
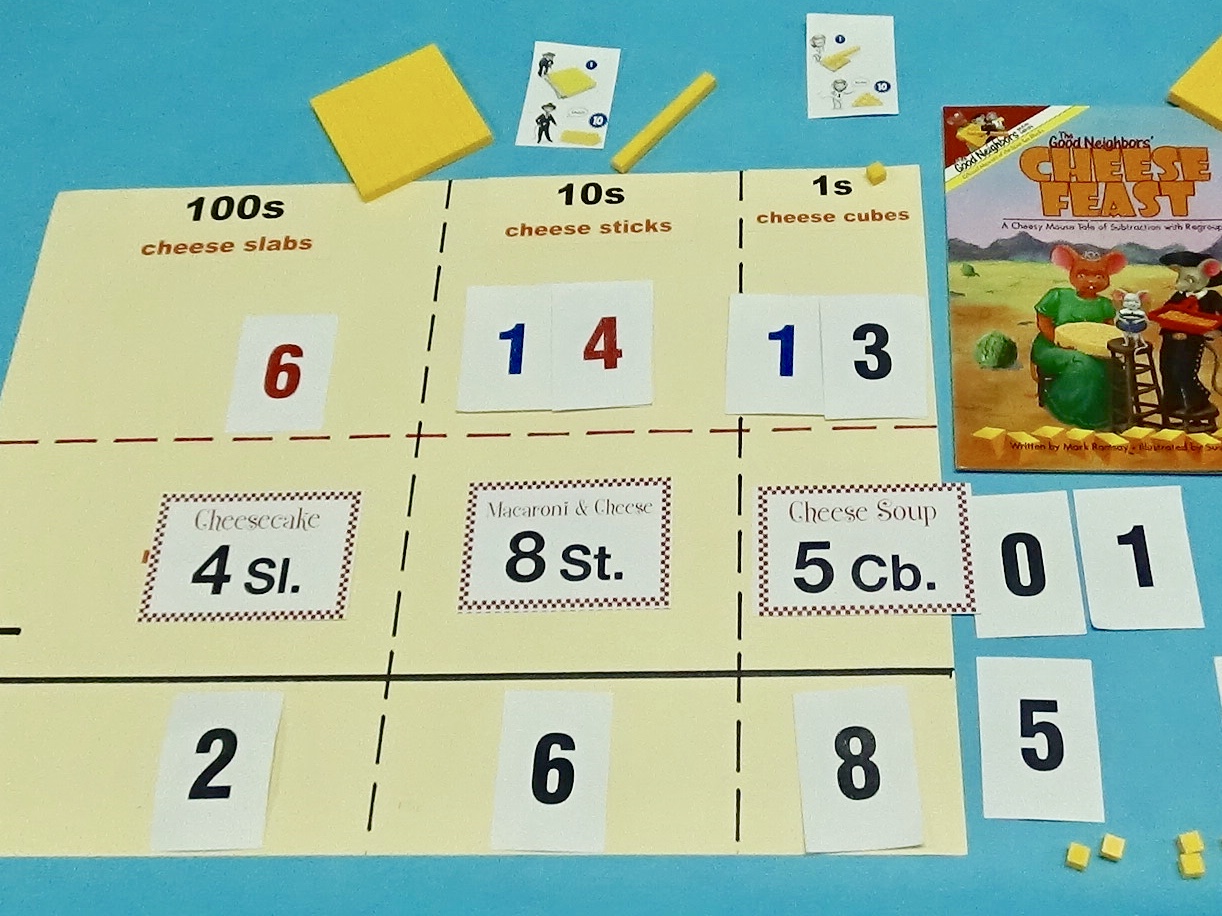
Read the book The Good Neighbors’ Cheese Feast.
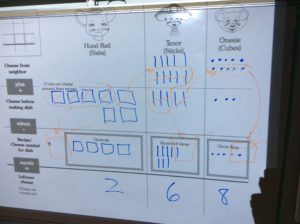
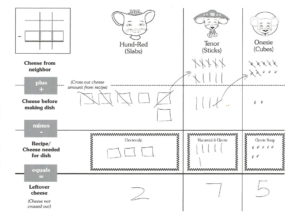
The book engages the students in the subject of subtraction, and it provides the students with a real-life schema for the subtraction process – cooking/baking, and more specifically the subtraction with regrouping process – cooking/baking with limited resources. The book gives a narrative (step-by-step order) for the subtraction algorithm. The book also provides scaffolding for several elements of place value and the subtraction process (ie. character names are similar to the place value names, the blocks of cheese resemble the hundreds, tens and ones base ten blocks, the characters’ house location corresponds to the order of the place values, the characters’ houses can only hold up to 9 blocks of cheese just as each place value can hold digits up to 9, the slicing of 1 bigger block of cheese into 10 smaller pieces of cheese).
Step 2
Model, and have students perform, the standard algorithm with base ten blocks.
Magnetic blocks work great for demonstrating the process, or use regular base ten blocks and project your model with a document camera. If you have a projector and magnetic blocks, model solving problems on The Good Neighbors Subtraction Template. The template provides extra scaffolding and prepares students it use the template in Step 3. After modeling, have students model the process with base ten blocks. A place value mat also works great for this and provides scaffolding for the process.
Step 3
Model, and have students perform, the process with base ten block notation.
Using real blocks can be challenging to manage, so I often move quickly to having students draw the blocks. I find using base ten block notation is just as or more effective than using the actual blocks. The Good Neighbors Subtraction Template is a useful tool because it provides scaffolding (characters for place value names and order of place values) that doesn’t otherwise exist.
Step 4
Model, and have students perform, the process using the ‘Hybrid Method‘.
The ‘Hybrid Method’ allows students to bridge the gap between solving the standard algorithm with drawings (concrete), and solving the standard algorithm with numerals (abstract). The ‘Hybrid Method’ uses number cards and key thumbnail pictures cards from the story to maintain the conceptual elements of the algorithm. Have students solve subtraction computations using the ‘Hybrid Method’. It is essential that students think aloud as they perform the method. After a few times using the ‘Hybrid Method’, students are generally able to visualize and verbalize the conceptual elements of the standard algorithm, and are ready to move to Step 5.
Step 5
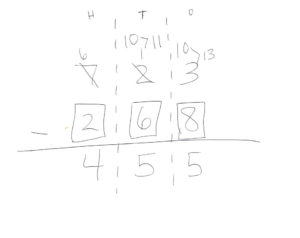
Model, and have students perform, the subtraction with regrouping process with numerals.
Begin using The Good Neighbors Subtraction Template for the reasons mentioned above. Have students think aloud all aspects of the algorithm including the cooking/baking scenario. Have the number and thumbnail pictures cards available to use as a model or as a resource students can use when first beginning to attempt the paper/pencil process. When student become comfortable with the process using the template, move to a basic Hundreds, Tens, Ones (HTO) template with plenty of room for students to show their work. Draw, and eventually have students draw, a rectangular border around each digit in the minuend to represent the recipe card in the subtraction cooking/baking schema. Eventually, have students solve computations with no template, but encourage them to continue to draw a rectangular border around each digit in the minuend to maintain the subtraction-cooking/baking schema.
Conclusion
Follow these 5 steps, and I guarantee students will solve subtraction computations accurately and efficiently. Just as important, students will have a conceptual understanding of the process, and they will be able to explain, mathematically, the steps they performed.
References
Wu, H. (2009) What’s Sophisticated About Elementary Mathematics? American Educator, Vol 33, NO.3.

Just want to emphasize I am thrilled that i stumbled on the website.
Thanks for the comment. Glad you found the content useful. Please follow us on Pinterest, we will be posting a lot of new content in the coming months.