5 ‘Novel’ Steps to Teach Addition with Regrouping – Conceptually

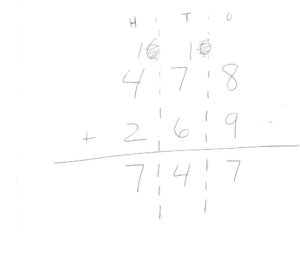
STEP 1

Read the book The Good Neighbors Store an Award.

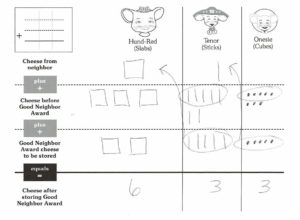
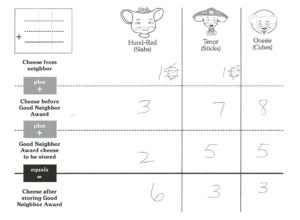
The book engages students in the subject of addition, and it provides a schema for addition – storing/combining two quantities; and specifically, addition with regrouping – storing/combining two quantities in limited space. The story’s narrative provides a step-by-step order for the addition algorithm.  The book also provides scaffolding for several elements of place value and the addition process (ie. character names are similar to the place value names, the blocks of cheese resemble the hundreds, tens and ones base ten blocks, the characters’ house location corresponds to the order of the place values, the characters’ houses can only store up to 9 blocks of cheese just as each place value can hold a digit up to 9). 

Step 2

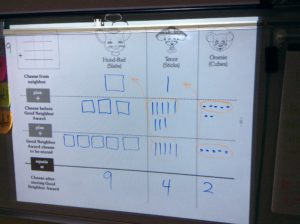
Model, and have students perform, the standard algorithm with base ten blocks.

Magnetic blocks work great for demonstrating the process, or use regular base ten blocks and project your model with a document camera.  If you have a projector and magnetic blocks, model solving problems on The Good Neighbors Addition Template. The template provides extra scaffolding and prepares students it use the template in Step 3. After modeling, have students model the process with base ten blocks.  A place value mat also works great for this and provides scaffolding for the process. 

Step 3

Model, and have students perform, the process with base ten block notation.

Using real blocks can be challenging to manage, so I often move quickly to having students draw the blocks.  I find using base ten block notation is just as or more effective than using the actual blocks.  The Good Neighbors Addition Template is a useful tool because it provides scaffolding (characters for place value names and order of place values) that doesn’t otherwise exist.

Step 4

Model, and have students perform, the process using the ‘Hybrid Method‘.

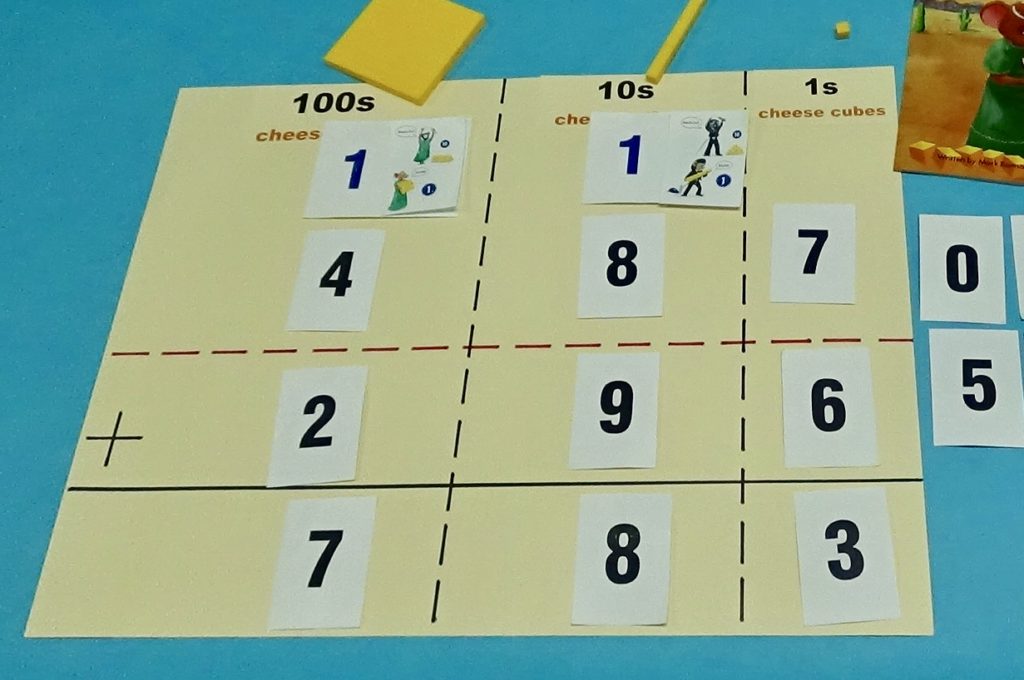
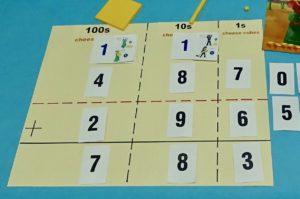
The ‘Hybrid Method’ allows students to bridge the gap between solving the standard algorithm with drawings (concrete), and solving the standard algorithm with numerals (abstract).  The ‘Hybrid Method’ uses number cards and key thumbnail pictures cards from the story to maintain the conceptual elements of the algorithm.  Have students solve addition computations using the ‘Hybrid Method’.  It is essential that students think aloud as they perform the method.  After a few times using the ‘Hybrid Method’, students are generally able to visualize and verbalize the conceptual elements of the standard algorithm, and are ready to move on to Step 5.

Step 5

Model, and have students perform, the addition with regrouping process with numerals.

Begin using The Good Neighbors Addition Template for the reasons mentioned above. Have students think aloud all aspects of the algorithm.  Have the number and thumbnail pictures cards available to use as a model or as a resource students can use when first beginning to attempt the paper/pencil process. When student become comfortable with the process using the template, move to a basic Hundreds, Tens, Ones (HTO) template with plenty of room for students to show their work. Eventually, have students solve computations with no template, but encourage them to continue to think aloud (or silently) the conceptual elements/steps of the algorithm. 

Conclusion 

Follow these 5 steps, and I guarantee students will solve addition computations accurately and efficiently. Just as important, students will have a conceptual understanding of the process, and they will be able to explain, mathematically, the steps they performed.